Rastgelelik ve Fisher Yates

Canımın aşırı sıkılması sonucunda cevabını bildiğim bir şeyin doğruluğunu test etmek için kolları sıvadım.

Bugünkü algoritmamız bir diziyi yerınde shuffle ettiğini iddaa ediyor. Diziyi sondan başa gezerken bulunduğunuz index ile gittiğiniz yöndeki kalan elemanlardan rastgele birisini swap ediyoruz. Döngü sonucunda shuffle edilmiş array elde ediyoruz. Literatür de fisher-yates veya knuth shuffle olarak geçiyor.

Her bir konfigurasyonun eşit olasılıklı olduğunu görmek istiyoruz. Dizideki her bir elemanı seçme ihtimalimiz 1/kalanlisteboyutu ise

ilk elemanı seçmek 1/n
ikinci eleman 1/n-1
.
.
.
1

Tüm bunları çarpalım.

$$P(Konfigurasyon) = \frac{1}{n} * \frac{1}{n-1} * \frac{1}{n-2} * \cdots * \frac{1}{2}* 1 = \frac{1}{n!} $$

Demekki her bir konfigurasyonun gelme ihtimali 1/n! imiş. Şunu yapmamız da mümkün, bir sürü deney yapıp her bir konfigurasyondan kaç tane geldiğini sayarız. Bunun uniform dağılmış olmasını bekliyoruz.

Şimdi de bir elemanın hangi ihtimalle kaçıncı indexte olacağını hesaplamaya geldi.

$$P(index) = \frac{n-1}{n} * \frac{n-2}{n-1} * \frac{n-3}{n-2} * \cdots * \frac{1}{2}* 1 = \frac{1}{n} $$

Her bir elemanın 0. indexte olması ihtimali 1/n miş. Sonraki elemanın İsterseniz görsel ispatına da bakabilirsiniz.

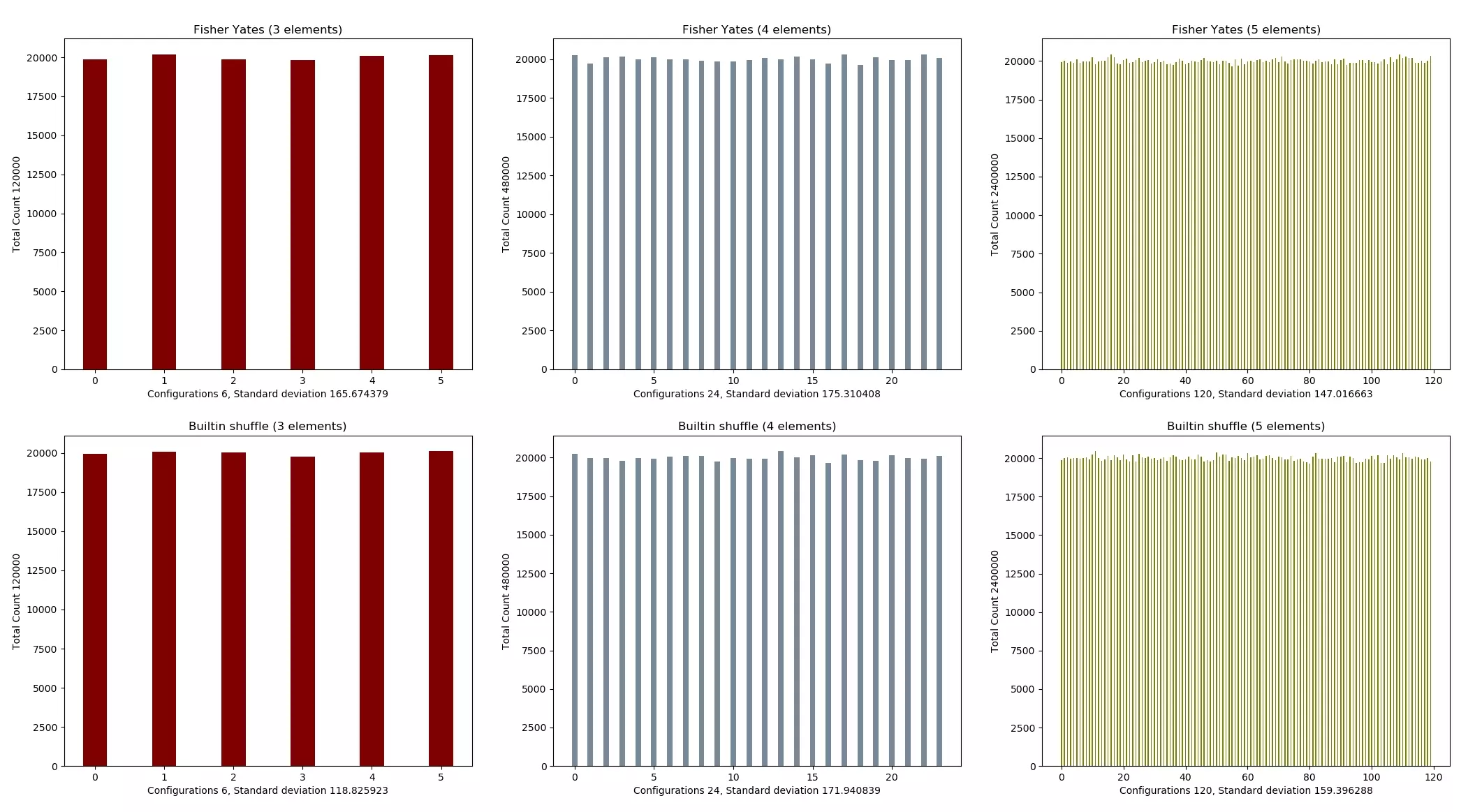
İspat kısmımız bittiğine göre gelelim grafiklere. 3, 4, 5 elemanlı diziler için python ın builtin ve fisher yates algoritması ile karıştırılmış varyasyonlar ı görselleştirelim.

Her bir diziyi medyana göre normalize etmeden standart sapma hesapladığım için büyük bir değer çıkması normal. Kıyaslamayı pythonın builtin shuffle fonksiyonuna göre yaptığımız için çok önemli değil.

Fisher yates algoritmasının özellikleri

• Unbiased
• İmplement etmesi basit
• Her bir konfigurasyon eşit olasılıklı
• In place çalışıyor

Daha ne olsun.

Böyle bir analiz yapmak durumunda kalırsınız diye kodları paylaşıyorum.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

from math import factorial
from random import shuffle, choice
from collections import Counter
from statistics import stdev
import matplotlib.pyplot as plt

def fisher_yates(A):
    for i in xrange(len(A) - 1, -1, -1):
        j = choice(range(i + 1))
        A[i], A[j] = A[j], A[i]

def get_freq(arr, shuffle_algo, cnt):
    permutation_count = factorial(len(arr))
    enumerations = range(permutation_count)
    l = []
    for i in range(cnt):
        shuffle_algo(arr)
        l.append(int(''.join([str(i) for i in arr])))
    return enumerations, Counter(l).values()

def sub_chart(plot_number, arr, title, algo, count, color):
    plt.subplot(2, 3, plot_number)
    keys, bars = get_freq(arr, algo, count)
    plt.title(title)
    plt.xlabel("Configurations %d, Standard deviation %f" % (factorial(len(arr)), stdev(bars)))
    plt.ylabel("Total Count %d" % count)
    plt.bar(keys, bars, color=color, width=0.35)

x = 20000
sub_chart(1, [1, 2, 3], "Fisher Yates (3 elements)", fisher_yates, 6 * x, 'maroon')
sub_chart(2, [1, 2, 3, 4], "Fisher Yates (4 elements)", fisher_yates, 24 * x, 'lightslategray')
sub_chart(3, [1, 2, 3, 4, 5], "Fisher Yates (5 elements)", fisher_yates, 120 * x, 'olive')
sub_chart(4, [1, 2, 3], "Builtin shuffle (3 elements)", shuffle, 6 * x, 'maroon')
sub_chart(5, [1, 2, 3, 4], "Builtin shuffle (4 elements)", shuffle, 24 * x, 'lightslategray')
sub_chart(6, [1, 2, 3, 4, 5], "Builtin shuffle (5 elements)", shuffle, 120 * x, 'olive')
plt.show()