Friend Circles

Soru: Bir grup insan birbiri ile arkadaş oluyor, Arkadaşlıklar geçişken olduğuna göre verilen input sonucu kaç tane farklı arkadaşlık networku oluşur. Geçişkenliğin tanımını yapalım A ile B, B ile C arkadaş ise A ile C arkadaştır.

Çözüm

Klasik bir disjoint set problemi. Her bir arkadaşlık ekleme(merge) işlemi yaparken iki kişi aynı networkte değilse network sayısı bir azalır.

Çözüm alternatifi olarak her bir insan için dfs-visit çalıştırıp her bir connected component için network sayısını her seferinde bir artırabilirsiniz.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <bits/stdc++.h>
using namespace std;

int c;
int solve(vector<vector<int>>& M) {
    int n = M.size();
    c = n;
    
    vector<int> v(n);
    for(int i = 0 ; i < n ; i++) v[i] = i;
    
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            if (M[i][j] == 1 && i != j)
                merge(v, i, j);
    
    return c;
}

int root(vector<int>& v, int x){ 
    return v[x] == x ? x : v[x] = root(v, v[x]);
}

void merge(vector<int>& v, int a, int b){
    int x = root(v, a);
    int y = root(v, b);
    
    if( x != y )
        v[x] = y, c--;
}

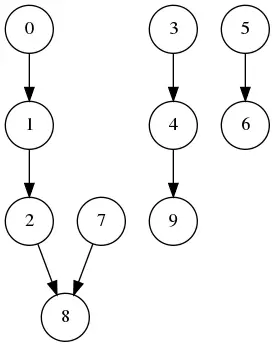
Görselleştirmesini graphviz kullarak yapalım.

union find

Graphviz çizimini nasıl yaptığıma dair kodu buraya bırakıyorum.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

from graphviz import Digraph, Graph

dot = Digraph(format='png')
N = 10
id = range(10)

for i in id:
    dot.node(str(i), shape="circle")

def root(i):
    while i != id[i]:
        id[i] = id[id[i]]
        i = id[i]

    return i

def union(id, p, q):
    i = root(p)
    j = root(q)
    id[i] = j
    dot.edge(str(i), str(j))


def find(id, p, q):
    return root(p) == root(q)

union(id, 0, 1)
union(id, 1, 2)
union(id, 3, 4)
union(id, 5, 6)
union(id, 7, 8)
union(id, 3, 9)
union(id, 1, 8)

print find(id, 1, 6)

dot.render("graph.gv")
« Trapping Rain Water
Asal Sayı Problemi »